今回は、VAEを使った最新の画像異常検知について理解してみます。
こんにちは cedro です。
以前 、オートエンコーダーを使って、ノイズ除去やメガネ女子のメガネ除去をやってみました。いずれも、入力画像に今まで学習したことがない物が含まれていると、その物は出力画像に再現出来ないという性質を利用したものです。
この性質を発展させると、正常品の画像のみをオートエンコーダーに学習させておくと、入力に異常品の画像が入った時に異常検知が出来ることになります。しかも、学習時の正常品の画像は、ラベル付けの必要がなく、とても使い勝手が良いと思っていました。
そうした中、最近、VAEを使った画像の異常検知について最新の論文の内容を実装している興味深いブログを見つけました。まだ、自分にとってはとても難しいレベルなのですが、自分なりに読み解いてなんとか理解したいと思います。
ということで、今回は、VAEを使った最新の画像異常検知について理解してみます。
論文のポイント
今回題材にする論文は、深層生成モデルによる非正則化異常度を用いた工業製品の異常検知 です。内容は、複雑な工業製品の画像を対象にした高精度な異常検知方法の提案です。
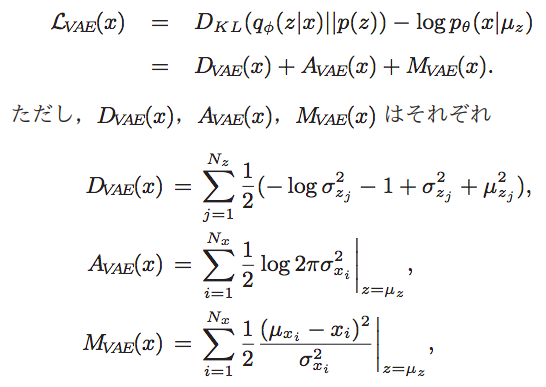
これは論文からの引用です。VAE は、損失関数 Lvae(x) = Dave(x) + Avae(x) + Mvae(x) と3つの項から構成されています。1つ目 Dvae(x) は、与えられたデータの中から頻度の高い特徴を学習し、頻度の少ない特徴を無視する性質を持つ項。2つ目 Avae(x) は、与えられたデータの中の特徴の複雑さに応じて調整する性質を持つ項。そして3つ目 Mvae(x) は、直接的に再現誤差に関係している項です。
ご存知の様に、VAE は高次元の空間にあるデータを低次元の潜在空間に、特徴量を連続的に滑らかに写像させることを狙いとしています。こういう場合は、Dave(x) や Avae(x) が有効に機能するわけです。
しかし、複雑な工業製品の画像の異常検知を行う場合は、検出したい異常は頻度が低く、様々な種類の要素(平らな表面、曲がった部分、ネジの穴など)から構成されているため複雑さも高いです。なので、Dave(x) や Avae(x) の項目は異常かどうかを判定するための閾値を変化させてしまいます。従って、こういう場合は、Dave(x) や Avae(x) の項目は削除し、損失関数 Lvae(x) = Mvae(x) だけで良いと言うのが、論文の主張です。
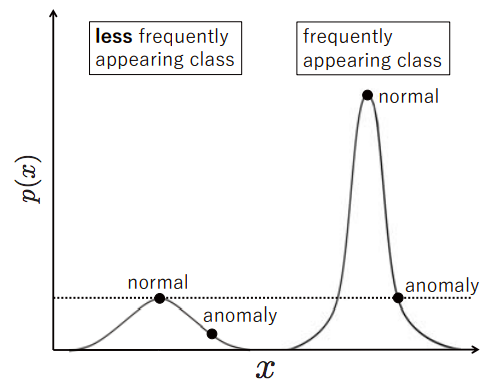
これも論文からの引用です。これは、Dave(x) や Avae(x) があると、特徴量の出現頻度によって異常検知の閾値が変化してしまうということを示す概念図です。出現頻度が高い場合の閾値は相対的に高く、出現頻度が低い場合の閾値は相対的に低くなります。
実装します
論文では、モノクロ640×480のネジ穴画像を使って実験しています。学習時は、640×640の正常画像からランダムに96×96のサイズを切り出して学習を行います。テスト時は、640×640の正常・異常画像から96×96サイズを16ピクセル間隔で切り出して異常度を算出し、少なくとも1枚が閾値を越えていたら異常と判断しています。
今回は、これをmnist で実装してみます。正常画像は「1」、異常画像を「9」とします。学習時は、28×28の正常画像「1」の画像からランダムに8×8サイズを100,000枚切り出して学習を行います。テスト時は、28×28の正常画像「1」1枚と異常画像「9」1枚から8×8サイズを2ピクセル間隔で切り出して異常度を算出します。まだ閾値は設定せず、上手く検出できるかどうか見るために可視化のみ行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 8×8のサイズに切り出す関数 def cut_img(x, number, height=8, width=8): print("cutting images ...") x_out = [] for i in range(number): shape_0 = np.random.randint(0,x.shape[0]) shape_1 = np.random.randint(0,x.shape[1]-height) shape_2 = np.random.randint(0,x.shape[2]-width) temp = x[shape_0, shape_1:shape_1+height, shape_2:shape_2+width, 0] x_out.append(temp.reshape((8, 8, 1))) print("Complete.") x_out = np.array(x_out) return x_out |
28×28画像から8×8サイズを切り出す関数 cut_img() です。引数は、x = 元画像データ、number = 切り出す枚数です。
8-10行目で、shape_0 、shape_1、 shape_2 に適切な範囲のランダムな整数を入れます。11行目で、temp = x [ shape_0, shape_1:shape_1+height, shape_2:shape_2+width, 0 ] によって、temp にx画像から8×8サイズに切り出したデータが入ります。12行目で、x_out にtemp の結果をアペンドします。これをnumber 回繰り返すわけです。
この理屈は、単純化したサンプルコードを見ると分かりやすいので、下記に補足します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np # 5行5列のデータを作成 x = np.arange(25).reshape(5, 5) print(x);print() # (1, 5, 5, 1)にリシェイプ x = x.reshape(1, 5, 5, 1) # 2行3列を切り出す x = x[0, 0:2, 0:3, 0] print(x) |
5行5列のデータから2行3列のデータを切り出すサンプルコードです。これを、実行すると、
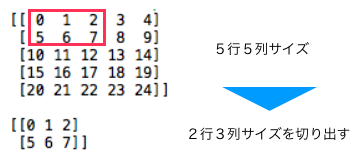
こんな結果になります。つまり、x = x [ 0, 0:2, 0:3, 0 ] で、左上角から2行×3列分データを切り出すことになるわけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# データセットの読み込み (x_train, y_train), (x_test, y_test) = mnist.load_data() #(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data() # Fashion MNIST x_train = x_train.reshape(x_train.shape[0], 28, 28, 1) x_test = x_test.reshape(x_test.shape[0], 28, 28, 1) x_train = x_train.astype('float32') / 255 x_test = x_test.astype('float32') / 255 # 学習データの作成 x_train_1 = [] for i in range(len(x_train)): if y_train[i] == 1: # Fashion mnist の場合は7(スニーカー) x_train_1.append(x_train[i].reshape((28, 28, 1))) x_train_1 = np.array(x_train_1) # 8×8のサイズに切り出す関数を呼び出す x_train_1 = cut_img(x_train_1, 100000) print("train data:",len(x_train_1)) # 評価データの作成 x_test_1, x_test_9 = [], [] for i in range(len(x_test)): if y_test[i] == 1: # Fashion mnist の場合は7(スニーカー) x_test_1.append(x_test[i].reshape((28, 28, 1))) if y_test[i] == 9: x_test_9.append(x_test[i].reshape((28, 28, 1))) x_test_1 = np.array(x_test_1) x_test_9 = np.array(x_test_9) # test_normal画像(1)と test_anomaly画像(9)をランダムに選ぶ test_normal = x_test_1[np.random.randint(len(x_test_1))] test_anomaly = x_test_9[np.random.randint(len(x_test_9))] test_normal = test_normal.reshape(1, 28, 28, 1) test_anomaly = test_anomaly.reshape(1, 28, 28, 1) |
データセットを作成する部分です。3−8行目で、minist のデータセットを読み込みます。
11行目から学習データの作成です。学習には「1」のデータしか使わないので、データセットから「1」のみ抽出し、19行目で先程の関数を呼んで、x_train_1 に「1」からランダムに切り出した8×8サイズの画像を100,000枚格納します。
24行目から評価データの作成です。評価には「1」と「9」のデータを使うので、データセットから「1」と「9」を抽出します。最終的な評価には、test_normal にランダムに選んだ「1」を1枚格納し、test_anomaly にランダムに選んだ「9」を1枚格納します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
#ヒートマップの計算 def evaluate_img(model, x_normal, x_anomaly, name, height=8, width=8, move=2): img_normal = np.zeros((x_normal.shape)) img_anomaly = np.zeros((x_normal.shape)) for i in range(int((x_normal.shape[1]-height)/move)): for j in range(int((x_normal.shape[2]-width)/move)): x_sub_normal = x_normal[0, i*move:i*move+height, j*move:j*move+width, 0] x_sub_anomaly = x_anomaly[0, i*move:i*move+height, j*move:j*move+width, 0] x_sub_normal = x_sub_normal.reshape(1, height, width, 1) x_sub_anomaly = x_sub_anomaly.reshape(1, height, width, 1) #従来手法 if name == "old_": #正常のスコア normal_score = model.evaluate(x_sub_normal, batch_size=1, verbose=0) img_normal[0, i*move:i*move+height, j*move:j*move+width, 0] += normal_score #異常のスコア anomaly_score = model.evaluate(x_sub_anomaly, batch_size=1, verbose=0) img_anomaly[0, i*move:i*move+height, j*move:j*move+width, 0] += anomaly_score #提案手法 else: #正常のスコア mu, sigma = model.predict(x_sub_normal, batch_size=1, verbose=0) loss = 0 for k in range(height): for l in range(width): loss += 0.5 * (x_sub_normal[0,k,l,0] - mu[0,k,l,0])**2 / sigma[0,k,l,0] img_normal[0, i*move:i*move+height, j*move:j*move+width, 0] += loss #異常のスコア mu, sigma = model.predict(x_sub_anomaly, batch_size=1, verbose=0) loss = 0 for k in range(height): for l in range(width): loss += 0.5 * (x_sub_anomaly[0,k,l,0] - mu[0,k,l,0])**2 / sigma[0,k,l,0] img_anomaly[0, i*move:i*move+height, j*move:j*move+width, 0] += loss save_img(x_normal, x_anomaly, img_normal, img_anomaly, name) |
学習後に、テスト画像の評価結果を可視化する関数 evaluate_img() です。引数は、model = モデル名、x_noramal = 正常画像データ(1枚)、x_anomaly = 異常画像データ(1枚)、name = 従来手法(old)か提案手法(new)の選択です。
4−5行目で、8×8サイズの判定結果を順次上書きするための28×28サイズを「0」で埋めた配列 img_normal、img_anomaly を作ります。
7−12行目で、x_nomal (正常画像)から8×8サイズを切り出したものをx_sub_nomal に格納し、x_anomaly(異常画像) から8×8サイズを切り出したものをx_sub_anomaly に格納します。そして、これを行方向、列方向の両方で、2ピクセル間隔で順次行います。
15-22行目は、従来手法による計算です。17行目で x_sub_normal のスコア(nomal_score)を計算し、18行目で先程作成した img_normal に上書きします(8行8列には同じスコアが加算されます)。x_sub_anomalyの場合も同様です。
27−40行目は、提案手法による計算です。29−31行目で、Mvae(x) を計算するために、x_sub_normal について変数 loss = 0.5*(x_sub_normal – mu) **2 / sigma を1ピクセル単位で計算し、loss に累計します。32行目で、先程作成した img_normal にこれを上書きします(8行8列には同じloss値が加算されます)。x_sub_anomalyの場合も同様です。
コードを動かしてみます。
学習データが100,000個ありますが、モノクロ28×28なので、ノートパソコンでも軽快に動きます。私のMacbookAirでは、26 sec/epoch で、10epoch を4分ちょっとで完了しました。
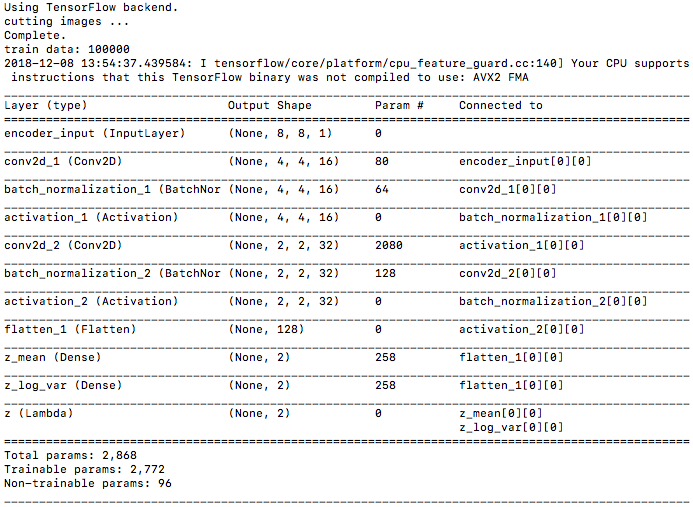
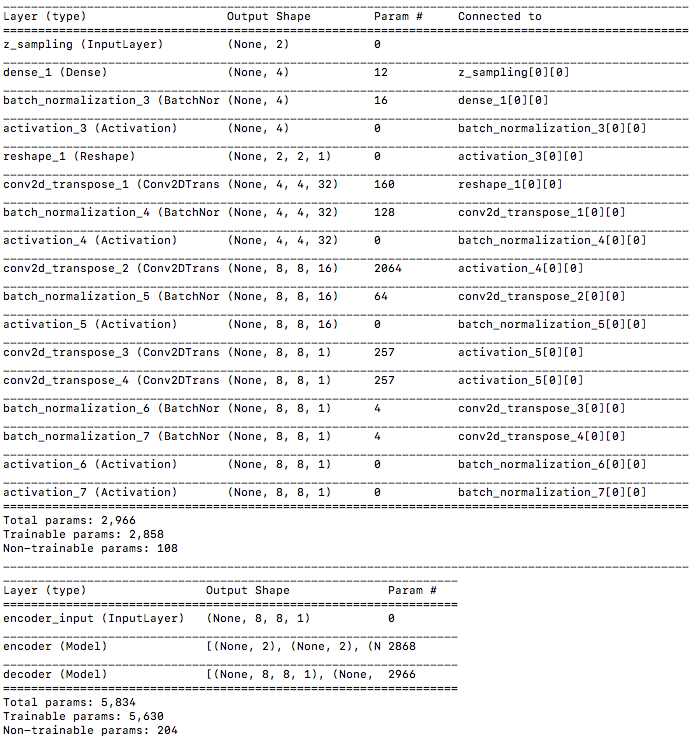
コードを実行すると、まずモデルサマリーが、Encoder、Decoder、VAE と表示され、学習を開始します。
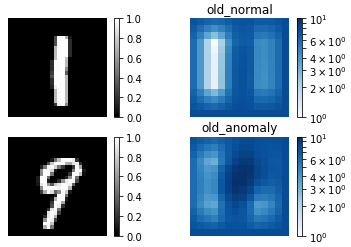
従来手法(old)による異常検出結果です。normal(正常画像)とanomaly(異常画像)による差があまりありません。これでは、適切な閾値の設定は難しく、検出精度はあまり期待出来ません。
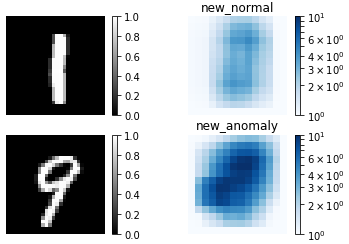
提案手法(new)による異常検出結果です。normal(正常画像)とanomaly(異常画像)による差が明確です。これなら、適切な閾値を設定すれば、結構高い検出精度が期待出来そうです。
コードのデータセットの読み込み部分を少し変更すると、Fashion _mnist でも直ぐ試せますので、やってみましょう。
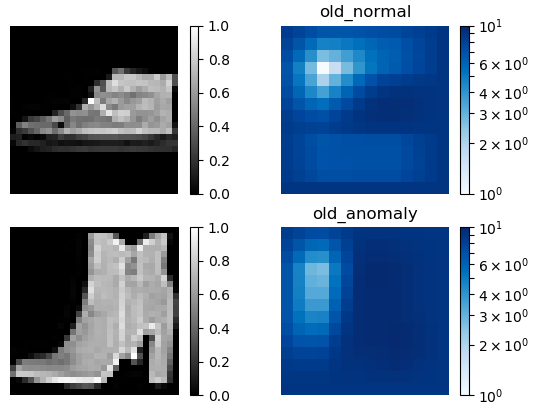
従来手法(old)による異常検出結果(7.スニーカーと9.ブーツ)です。やはり、normal(正常画像)とanomaly(異常画像)による差があまり無いです。
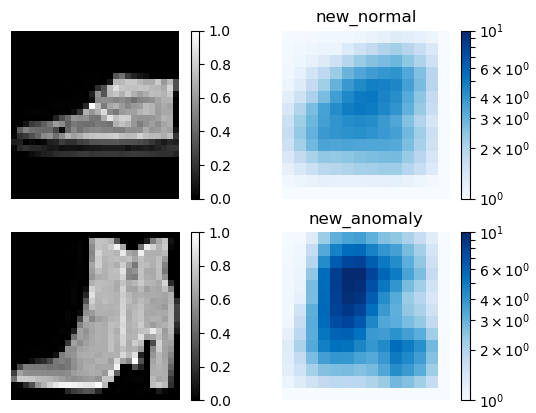
提案手法(new)による異常検出結果(7.スニーカーと9.ブーツ)です。normal(正常画像)とanomaly(異常画像)による差が明確です。
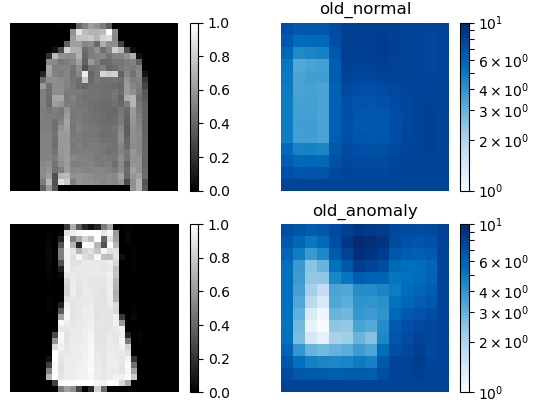
従来手法(old)による異常検出結果(2.セーターと3.ドレス)です。やはりイマイチです。
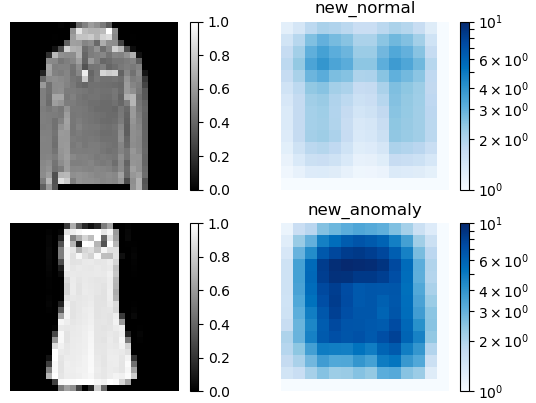
提案手法(new)による異常検出結果(2.セーターと3.ドレス)です。素晴らしい! 本当にこれ結構実用になりそうな気がします。
最後に、コード全体を載せておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 |
from __future__ import absolute_import from __future__ import division from __future__ import print_function from keras.layers import Lambda, Input, Dense, Reshape from keras.models import Model from keras.datasets import mnist from keras.datasets import fashion_mnist from keras.losses import mse from keras.utils import plot_model from keras import backend as K from keras.layers import BatchNormalization, Activation, Flatten from keras.layers.convolutional import Conv2DTranspose, Conv2D import numpy as np import matplotlib.pyplot as plt import matplotlib.colors as colors import os # 8×8のサイズに切り出す関数 def cut_img(x, number, height=8, width=8): print("cutting images ...") x_out = [] for i in range(number): shape_0 = np.random.randint(0,x.shape[0]) shape_1 = np.random.randint(0,x.shape[1]-height) shape_2 = np.random.randint(0,x.shape[2]-width) temp = x[shape_0, shape_1:shape_1+height, shape_2:shape_2+width, 0] x_out.append(temp.reshape((8, 8, 1))) print("Complete.") x_out = np.array(x_out) return x_out # データセットの読み込み (x_train, y_train), (x_test, y_test) = mnist.load_data() #(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data() x_train = x_train.reshape(x_train.shape[0], 28, 28, 1) x_test = x_test.reshape(x_test.shape[0], 28, 28, 1) x_train = x_train.astype('float32') / 255 x_test = x_test.astype('float32') / 255 # 学習データの作成 x_train_1 = [] for i in range(len(x_train)): if y_train[i] == 1: # スニーカーは7 x_train_1.append(x_train[i].reshape((28, 28, 1))) x_train_1 = np.array(x_train_1) # 8×8のサイズに切り出す関数を呼び出す x_train_1 = cut_img(x_train_1, 100000) print("train data:",len(x_train_1)) # 評価データの作成 x_test_1, x_test_9 = [], [] for i in range(len(x_test)): if y_test[i] == 1: # スニーカーは7 x_test_1.append(x_test[i].reshape((28, 28, 1))) if y_test[i] == 9: x_test_9.append(x_test[i].reshape((28, 28, 1))) x_test_1 = np.array(x_test_1) x_test_9 = np.array(x_test_9) # test_normal画像(1)と test_anomaly画像(9)をランダムに選ぶ test_normal = x_test_1[np.random.randint(len(x_test_1))] test_anomaly = x_test_9[np.random.randint(len(x_test_9))] test_normal = test_normal.reshape(1, 28, 28, 1) test_anomaly = test_anomaly.reshape(1, 28, 28, 1) # reparameterization trick # instead of sampling from Q(z|X), sample eps = N(0,I) # z = z_mean + sqrt(var)*eps def sampling(args): z_mean, z_log_var = args batch = K.shape(z_mean)[0] dim = K.int_shape(z_mean)[1] # by default, random_normal has mean=0 and std=1.0 epsilon = K.random_normal(shape=(batch, dim)) return z_mean + K.exp(0.5 * z_log_var) * epsilon # network parameters input_shape=(8, 8, 1) batch_size = 128 latent_dim = 2 epochs = 10 ### Nc = 16 # build encoder model inputs = Input(shape=input_shape, name='encoder_input') x = Conv2D(Nc, kernel_size=2, strides=2)(inputs) x = BatchNormalization()(x) x = Activation('relu')(x) x = Conv2D(2*Nc, kernel_size=2, strides=2)(x) x = BatchNormalization()(x) x = Activation('relu')(x) x = Flatten()(x) z_mean = Dense(latent_dim, name='z_mean')(x) z_log_var = Dense(latent_dim, name='z_log_var')(x) z = Lambda(sampling, output_shape=(latent_dim,), name='z')([z_mean, z_log_var]) encoder = Model(inputs, [z_mean, z_log_var, z], name='encoder') encoder.summary() # build decoder model latent_inputs = Input(shape=(latent_dim,), name='z_sampling') x = Dense(2*2)(latent_inputs) x = BatchNormalization()(x) x = Activation('relu')(x) x = Reshape((2,2,1))(x) x = Conv2DTranspose(2*Nc, kernel_size=2, strides=2, padding='same')(x) x = BatchNormalization()(x) x = Activation('relu')(x) x = Conv2DTranspose(Nc, kernel_size=2, strides=2, padding='same')(x) x = BatchNormalization()(x) x = Activation('relu')(x) x1 = Conv2DTranspose(1, kernel_size=4, padding='same')(x) x1 = BatchNormalization()(x1) out1 = Activation('sigmoid')(x1)#out.shape=(n,8,8,1) x2 = Conv2DTranspose(1, kernel_size=4, padding='same')(x) x2 = BatchNormalization()(x2) out2 = Activation('sigmoid')(x2)#out.shape=(n,8,8,1) decoder = Model(latent_inputs, [out1, out2], name='decoder') decoder.summary() # build VAE model outputs_mu, outputs_sigma_2 = decoder(encoder(inputs)[2]) vae = Model(inputs, [outputs_mu, outputs_sigma_2], name='vae_mlp') vae.summary() # VAE loss m_vae_loss = (K.flatten(inputs) - K.flatten(outputs_mu))**2 / K.flatten(outputs_sigma_2) m_vae_loss = 0.5 * K.sum(m_vae_loss) a_vae_loss = K.log(2 * 3.14 * K.flatten(outputs_sigma_2)) a_vae_loss = 0.5 * K.sum(a_vae_loss) kl_loss = 1 + z_log_var - K.square(z_mean) - K.exp(z_log_var) kl_loss = K.sum(kl_loss, axis=-1) kl_loss *= -0.5 vae_loss = K.mean(kl_loss + m_vae_loss + a_vae_loss) vae.add_loss(vae_loss) vae.compile(optimizer='adam') # train the autoencoder vae.fit(x_train_1, epochs=epochs, batch_size=batch_size) #validation_data=(x_test, None)) vae.save_weights('vae_mlp_mnist.h5') ### 学習後の検出テスト ### #ヒートマップの計算 def evaluate_img(model, x_normal, x_anomaly, name, height=8, width=8, move=2): ####### img_normal = np.zeros((x_normal.shape)) img_anomaly = np.zeros((x_normal.shape)) for i in range(int((x_normal.shape[1]-height)/move)): for j in range(int((x_normal.shape[2]-width)/move)): x_sub_normal = x_normal[0, i*move:i*move+height, j*move:j*move+width, 0] x_sub_anomaly = x_anomaly[0, i*move:i*move+height, j*move:j*move+width, 0] x_sub_normal = x_sub_normal.reshape(1, height, width, 1) x_sub_anomaly = x_sub_anomaly.reshape(1, height, width, 1) #従来手法 if name == "old_": #正常のスコア normal_score = model.evaluate(x_sub_normal, batch_size=1, verbose=0) img_normal[0, i*move:i*move+height, j*move:j*move+width, 0] += normal_score #異常のスコア anomaly_score = model.evaluate(x_sub_anomaly, batch_size=1, verbose=0) img_anomaly[0, i*move:i*move+height, j*move:j*move+width, 0] += anomaly_score #提案手法 else: #正常のスコア mu, sigma = model.predict(x_sub_normal, batch_size=1, verbose=0) loss = 0 for k in range(height): for l in range(width): loss += 0.5 * (x_sub_normal[0,k,l,0] - mu[0,k,l,0])**2 / sigma[0,k,l,0] img_normal[0, i*move:i*move+height, j*move:j*move+width, 0] += loss #異常のスコア mu, sigma = model.predict(x_sub_anomaly, batch_size=1, verbose=0) loss = 0 for k in range(height): for l in range(width): loss += 0.5 * (x_sub_anomaly[0,k,l,0] - mu[0,k,l,0])**2 / sigma[0,k,l,0] img_anomaly[0, i*move:i*move+height, j*move:j*move+width, 0] += loss save_img(x_normal, x_anomaly, img_normal, img_anomaly, name) #ヒートマップの描画 def save_img(x_normal, x_anomaly, img_normal, img_anomaly, name): path = 'images/' if not os.path.exists(path): os.mkdir(path) # ※注意 評価したヒートマップを1~10に正規化 img_max = np.max([img_normal, img_anomaly]) img_min = np.min([img_normal, img_anomaly]) img_normal = (img_normal-img_min)/(img_max-img_min) * 9 + 1 img_anomaly = (img_anomaly-img_min)/(img_max-img_min) * 9 + 1 plt.figure() plt.subplot(2, 2, 1) plt.imshow(x_normal[0,:,:,0], cmap='gray') plt.axis('off') plt.colorbar() plt.subplot(2, 2, 2) plt.imshow(img_normal[0,:,:,0], cmap='Blues',norm=colors.LogNorm()) plt.axis('off') plt.colorbar() plt.clim(1, 10) plt.title(name + "normal") plt.subplot(2, 2, 3) plt.imshow(x_anomaly[0,:,:,0], cmap='gray') plt.axis('off') plt.colorbar() plt.subplot(2, 2, 4) plt.imshow(img_anomaly[0,:,:,0], cmap='Blues',norm=colors.LogNorm()) plt.axis('off') plt.colorbar() plt.clim(1, 10) plt.title(name + "anomaly") plt.savefig(path + name +".png") plt.show() plt.close() #従来手法の可視化 evaluate_img(vae, test_normal, test_anomaly, "old_") #提案手法の可視化 evaluate_img(vae, test_normal, test_anomaly, "new_") |
さて、今回大変お世話になったブログは、「Variational Autoencoder を使った画像の異常検知 前編」です。深く感謝致します! いやー、それにしても、私の実力ではトレースするだけで精一杯でした(笑)。
なお、コードは自分で理解しやすい様に、オリジナルに対して順番を入れ替えたり表現を一部修正したりしています。
いつかは、自ら論文を読んで実装できる様になりたいものですが、それは見果ての夢かなー。
では、また。















コメントを残す